1838年，Ward在《人类骨科学》[1]提出了“Ward三角区”。Ward三角区是指内侧骨小梁系统和外侧骨小梁系统在股骨颈交叉的中心区形成一个三角区。基于Ward三角区，张英泽院士提出了大胆的假设：股骨头、颈及转子间骨小梁三角区远大于1个，即在股骨头、颈及转子间骨小梁三角区存在多个，因此将多个三角区命名为“张氏N三角理论”。骨小梁是松质骨中形成的一种支持性结缔组织成分。骨小梁在正常骨和愈合骨中都可形成。骨小梁的生长规律是沿着骨的应力线发展的，且最大骨小梁沿着最大应力线发展。起重机上梁的应力轨迹与各种人类骨骼中骨小梁的拱形模式之间的存在相似之处，导致了沃尔夫提出了骨小梁结构的轨迹假说，即“沃尔夫骨功能适应定律”或“沃尔夫定律”[2-3]。沃尔夫定律(Wolf′s Law)是指，骨在需要的地方就生长， 在不需要的地方就吸收，即是骨的生长、吸收、重建都与骨的受力状态有关[4]。股骨头、颈及转子间骨小梁是验证沃尔夫定律的小梁形态和“张氏N三角区”的很好的例子。基于von Meyer对股骨上端冠状切片的骨小梁轨迹结构描述[5-6]，股骨近端有5种类型的骨小梁，分别是主要张力小梁、主要压力小梁(内侧压力小梁)、次要压力小梁(外侧压力小梁)、次要张力小梁、大转子小梁。主要张力小梁呈弧形，从大转子的外侧边缘延伸到中央凹下方，弧形穿过股骨颈部的上部皮质和股骨头；主要是沿着拉伸/压缩应力的“线”(轨迹)，类似于顶点位于中性轴上的拱。主要压力小梁是垂直方向，呈三角形分布，从股骨头的内侧皮质延伸到股骨颈；主要是股骨头受外界压力形成的。次要压力小梁也是呈扇形分布，从股骨距和小转子延伸到大转子；主要是受来自小转子下方的压力形成的。由主要张力小梁、主要压力小梁及次要压力小梁三种小梁形态围成的中心区域称为Ward三角区，也就是Ward在183年前提到的经典三角区。但除此外，尚可观察到多个宏观三角区：① 由主要张力小梁、主要压力小梁及股骨头右下方边界围成的中心区域也为一个三角区；② 由主要张力小梁、主要压力小梁及股骨头右上方边界围成的中心区域也为一个三角区；③ 由主要张力小梁、主要压力小梁及股骨头左上方边界围成的中心区域也为一个三角区；④由主要张力小梁、大转子小梁及大转子上方边界围成的中心区域也为一个三角区；⑤ 由次要张力小梁、次要压力小梁及股骨内横向骨小梁围成的中心区域也为一个三角区等(图1)。这也是说明了除了Ward三角区，还存在其他三角区，从而验证了“张氏N三角理论”的合理性。为了再次验证“张氏N三角理论”存在性，本研究将从股骨头、颈及转子间骨小梁的数学模型来论证。
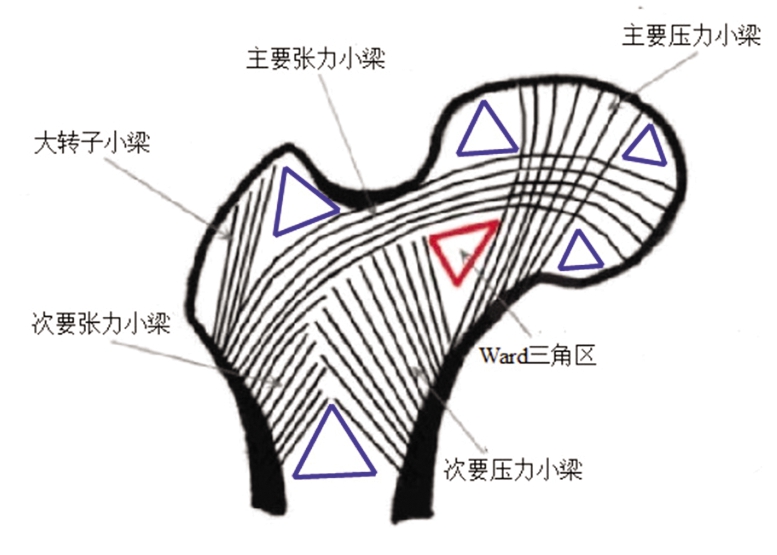
图1 股骨头、颈及转子间骨小梁三角区的结构示意图
1 建立股骨近端数学模型
建立简化的股骨近端数学模型，首先作出假设：①股骨颈没有前倾；②股骨颈直径R恒定及股骨干直径R1恒定；③股骨颈的长度h不变; ④股骨头的关节部分形成球体的一部分，股骨头半径r恒定；⑤股骨颈干角α恒定；⑥薄片是无限薄的。对于股骨近端数学模型，建立直角坐标系，以股骨颈的中心线为y轴，而x轴垂直于股骨颈中心线且x轴和y轴的交点位于股骨头的中心。在图2中，为了使拟合骨小梁曲线在股骨近端模型的空间中，需要获得点A、B、C、D的坐标点及股骨上、下颈的长度。首先假设CD=s；角ACD=β；则可以得到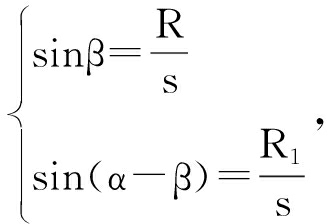
即得到
已知股骨颈直径R及股骨干直径R1恒定和股骨颈干角α恒定，这样就可以求得β的唯一角度，即可以获得H0=cotβ·R，则可以点A的坐标为
点B的坐标为
点C的坐标为[-R/2,-(h+1/2·cotβR)]；点D的坐标为[-R/2,-(h-1/2·cotβR)]。股骨上、下颈的长度分别为 AC=h+1/2·
虽然认识到这些假设在技术上并不真实，但提供了使模型最小化而开发数学解决方案所需的变量数量。在最小模型中，可能由骨小梁支撑的关节面的因素有股骨头半径r；股骨颈直径R；曲线与股骨颈皮质成θ角。图2显示了股骨近端数学模型。
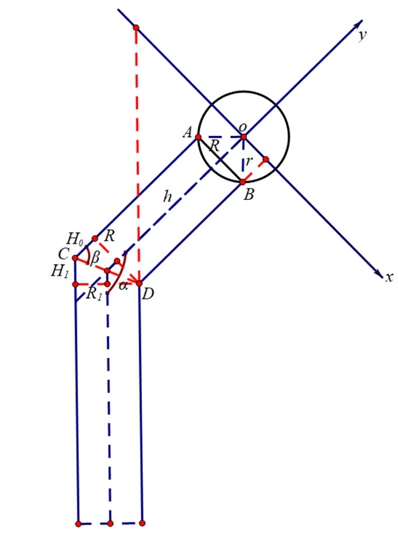
图2 股骨近端数学模型
2 拟合股骨头、颈及转子间骨小梁曲线
拟合股骨头、颈及转子间骨小梁曲线形成平滑曲线，与关节面软骨下板正交，且在与软骨下板相交处具有最大曲率，在与颈皮质相交处具有最小曲率[7]。
2.1 主要压力小梁的曲线方程：f(x)=ax2+bx+c 主要压力小梁的曲线与软骨下板的坐标(x,y)的坐标也满足极坐标(r cosφ,r sinφ)。曲线与股骨下颈皮质成θ角。函数y=f(x)隐含以下条件：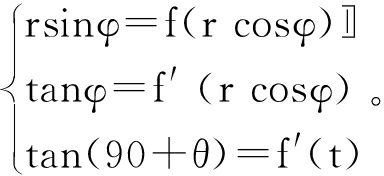
由消元法可到主要压力小梁的曲线如下：
其中s=tan(90+θ),t=R/2。
2.2 主要张力小梁的曲线方程：f(x)=Ax22+Bx+C 主要张力小梁的曲线与软骨下板的坐标(x,y)的坐标也满足极坐标(r cosφ,r sinφ)。曲线与股骨上颈皮质成θ1角。函数y=f(x)隐含以下条件：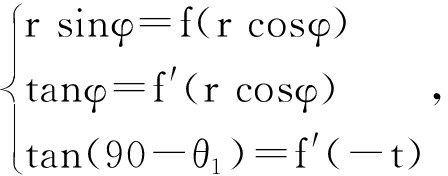
则可以得到主要张力小梁的曲线：
其中s=tan(90-θ1),t=R/2。
2.3 假设次要压力小梁的曲线方程：f(x)=a1x2+b1x+c1 次要压力小梁的曲线与股骨下颈皮质成θ角，曲线与股骨上颈皮质成θ1角。函数y=f(x)隐含以下条件：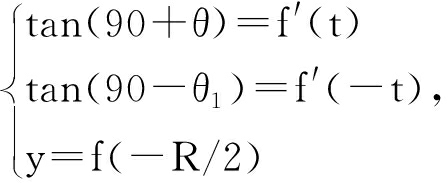
得到主要张力小梁的曲线：f(x)=
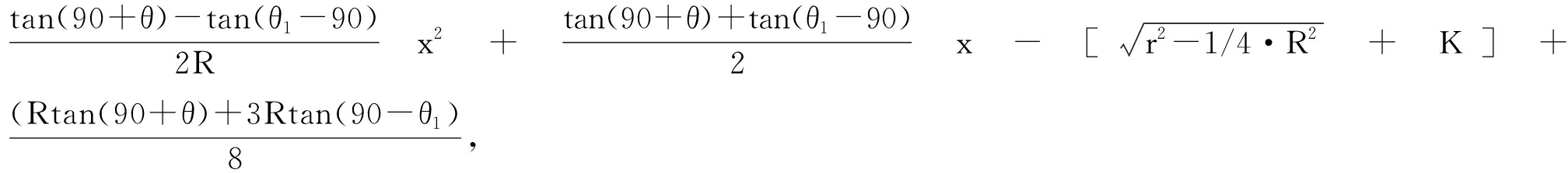其中K是常数。
在股骨头、颈及转子间三个骨小梁曲线的生理结构及假设条件的限制下，骨小梁结构的轨迹分布可以用Matlab软件来进行动态计算机模拟。模型涉及一些股骨近端的相关几何形态学参数，取这些参数的均值。已知股骨头半径r=23 mm；股骨颈直径R=34 mm；股骨干直径R1=36 mm；股骨颈的长度h=50 mm；股骨颈干角α=150 °；与软骨下板上的小梁间距设置为3 °。股骨头、颈及转子间三个骨小梁曲线在股骨近端最小模型内进行极限拟合，可以得到的拟合图(图3)。
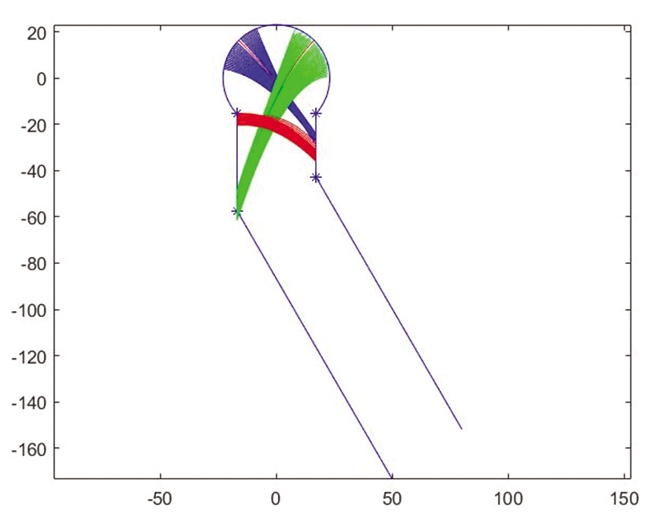
图3 股骨头、颈及转子间骨小梁曲线拟合
主要压力小梁、主要张力小梁及次要压力小梁曲线形成平滑曲线，且在与软骨下板相交处具有最大曲率，在与颈皮质相交处具有最小曲率。拟合的三个骨小梁曲线，有一定的生理结构限制，如主要压力小梁曲线与股骨下颈相交，主要压力小梁曲线与股骨上颈相交，次要压力小梁曲线在股骨下颈与股骨上颈之间。模型描述了且预测小梁可能存在的所有位置，揭示了关节软骨下板的任何暴露于载荷的区域必须由小梁充分支撑。除了Ward三角区，还存在其他四个三角区，从而论证了“张氏N三角理论”。在“张氏N三角理论”中，股骨近端存在数个“宏观三角”和无数个“微观三角”。这些三角衍架结构对于维持股骨近端骨性结构稳定性具有重要生理意义。基于“张氏N三角理论”和多年临床经验，张英泽院士课题组设计并研发出更符合人体力学传导特点的内固定物——股骨近端仿生髓内钉。“张氏N三角理论”对于骨折后内固定物的设计、研发、固定植入具有启发和指导意义。“张氏N三角理论”对于指导股骨相关手术[8]、预防术后并发症[9]及促进老年股骨骨折康复[10]都有一定的指导意义。
[1] Ward FO. Outlines of human osteology[M]. London:Henry Renshaw,1838:370.
[2] Wolff J. Ueber die innere architectur der knochen und ihre bedeutung für die frage vom knochenwachsthum[J]. Virchows Archiv Pathol Anat Physio,1870,50:389-450.
[3] Skedros JG，Brand RA. Biographical sketch:georg hermann von meyer(1815-1892)[J]. Clin Orthop Relat Res,2011,469(11):3072-3076.
[4] 武际可.结构工程师和骨科医生的产儿——沃尔夫定律[J]. 力学与实践,2014,36(6):798-801.
[5] Skedros JG，Baucom SL. Mathematical analysis of trabecular ′trajectories′ in apparent trajectorial structures:the unfortunate historical emphasis on the human proximal femur [J]. J Theor Biol,2007,244(1) :15-45.
[6] Von Meyer GH. Die Architekur der spongiosa [J]. Arch. Anat. Physiol. Wissenschaf. Med,1867,34:615-628.
[7] Field RE,Kenyon CM. A mathematical analysis for the modelling of trabecular bone [J]. J Biomed Eng,1989,5:384-389.
[8] 郭家良，王海立，董维冲，等.老年肱骨近端骨折的治疗与康复研究进展[J/CD].中华老年骨科与康复电子杂志,2019,5(4)：233-237.
[9] 刘大伟，牛帅.老年粗隆间骨折后发生下肢深静脉血栓的多因素分析[J/CD].中华老年骨科与康复电子杂志， 2020,6(3)：128-135.
[10] 董佩龙，唐晓波，王健，等.加速康复外科在人工股骨头置换术治疗老年股骨粗隆间骨折中的应用研究[J/CD].中华老年骨科与康复电子杂志，2021,7(3)：170-175.